HAALBAARHEIDSSTUDIE VOOR EEN HANGBRUG IN VVK MET EEN OVERSPANNING VAN 3,7 KM
door Kees van IJselmuijden Royal HaskoningDHV
Voor de E39 in Noorwegen is een brug nodig om de Sognefjord te kunnen passeren. Hiervoor is door de Noorse overheid een ontwerp gemaakt waarbij drie hangbruggen met elk een overspanning van 1.250 m met elkaar zijn verbonden. Bijzonder aan dit Noorse ontwerp is, dat de twee middelste pylonen drijvend zijn gefundeerd. De drijvende fundering is nodig, omdat het fjord 1.300 m diep is.
In de haalbaarheidsstudie van Royal HaskoningDHV wordt nagegaan of het fjord in één keer is te overspannen (3.700 m). De huidige ontwikkelingen in materialen maken het mogelijk om lichtere constructies voor bruggen te maken. Vezelversterkt Kunststof (VVK) is één van deze materialen. In deze studie worden de haalbaarheid en de toegevoegde waarde onderzocht van VVK door zowel het dek als de kabels uit te voeren met zoveel mogelijk kunststof. De voordelen van VVK ten opzichte van de traditionele materialen zijn de hoge sterkte, het geringe eigen gewicht en vooral de reductie van onderhoudskosten.
De belangrijkste punten die bij dit soort grote overspanningen een rol spelen, zijn de aerodynamica van het dek, de horizontale verplaatsing van het dek door windbelasting, de detaillering en gewicht van de hoofdkabels.
Om het ontwerp ook fraai vorm te geven, heeft Royal HaskoningDHVarchitect Joris Smits zijn visie op deze brug gegeven en daar wat schetsen aan toegevoegd.
De markt van extreem grote overspanningen voor bruggen is groeiende en omdat de huidige materialen tot het uiterste zijn toegepast, is het nodig om naar nieuwe materialen en mogelijkheden te kijken. VVK is één van deze materialen. Het materiaal heeft een veel hogere treksterkte en een lager gewicht dan staal. De langste brug op dit moment heeft een hoofdoverspanning van 1.991 m en ligt in Japan. De sprong van 1.991 m naar 3.700 m is enorm.
Eerdere studies [1,2,3,4] hebben aangetoond dat overspanningen van 3.700 m in traditionele materialen niet mogelijk zijn, omdat het gewicht van de staalkabels te groot zou worden. Daarentegen kan door de toepassing van lichtere materialen de aerodynamisch stabiliteit een probleem worden. Om dit te voorkomen, wordt het dek niet alleen lichter uitgevoerd maar ook stijf genoeg om de lagere stijfheid van VVK te verdisconteren.
UITGANGSPUNTEN
In deze haalbaarheidstudie kunnen we niet alles bekijken, daarom concentreren we ons op de volgende punten:
1 gewicht van het dek;
2 verticale verplaatsing;
3 spanningen in het VVK-dek en de Aramide kabels;
4 verschil tussen de 1e verticale frequentie en de torsiefrequentie.
HIERBIJ GAAN WE UIT VAN
• 5% extra eigengewicht om in de toekomst dempers te kunnen toepassen;
• voor horizontale stabiliteit wordt uitgegaan van een “twin-deck”;
• een windbelasting van 1,5 kN/m2;
• per dek wordt 100 mm asfalt over 8 m breedte toegepast;
• verkeersbelasting over 6 m breedte resulteert in een gelijkmatige belasting van 37,5 kN/m;
• horizontale verplaatsing L/200, gelijk als toegestaan voor de brug met drijvende pijlers [5] (horizontaal geen eis gevonden);
• dek uitgevoerd in VVK (met glasvezel);
• kabels uitgevoerd met Aramide vezels;
• verankering van de kabels in de rotsen is mogelijk;
• de pyloon zelf is niet beschouwd.
De uitdaging is om een constructie te ontwerpen met de juiste constructieeigenschappen, dat de verkeers- en windbelasting robuust kan weerstaan.
ANALYSE
Voor hangbruggen ligt de verhouding voor L/h tussen de 5 en 10. Om tot mooie ronde getallen te komen, gaan we hier uit van 3700m/450m = 8,22.
DEKCONSTRUCTIE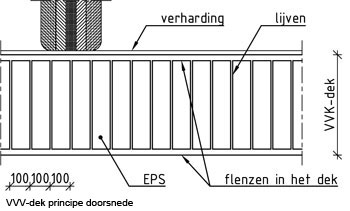
In Noorwegen zijn twee rijbanen genoeg voor deze weg met één vluchtstrook en een fietspad. Maar aangezien wij vanwege de stabiliteit gekozen hebben voor een twin deck, gaan we gemakshalve uit van 8 m asfalt op beide dekken en een dek van minimaal 10 m breed. Het originele enkele dek is 18,30 m breed en met 2 keer 10 passen we voor het dek niet veel materiaal extra toe, behalve de dwarsdragers. Tussen de dekken zit een ruimte van ca 25 m. De dekken worden in langsrichting om de 30 m met een dwarsdrager verbonden. Aan de dwarsdrager zit de verbinding met de hangkabels. Voor de dwarsdrager, die niet wordt geoptimaliseerd, wordt uitgegaan van staal.
RIJDEK
De hoogte van het rijdek wordt bepaald door de hart-op-hart afstand van de dwarsdragers die het rijdek ondersteunen. Er wordt zoveel mogelijk materiaal aan de buitenkant van de totale dekconstructie aangebracht, zodat dit efficiënt meedoet met de verticale stijfheid. Gekozen is het rijdek om de 1,5 m te ondersteunen met een dwarsdrager. Op basis van de doorbuigingseis van L/200 mag de doorbuiging van het rijdek niet meer zijn dan 1500/200 = 7,5 mm. Om praktische en globale stijfheidsredenen is een VVK dek van 150 mm gekozen. Voor het dek wordt uitgegaan van het principe van de vacuüm infusietechniek.
Op basis van een eenvoudige berekening van een overspanning op twee steunpunten (in plaats van een doorgaand dek), zijn de afmetingen gecontroleerd. Hiervoor wordt een bovengrens gebruikt, door het dek over een strook van 3 m breed te berekenen met hierop de verkeersbelasting van de Eurocode LM1 met puntlasten van 600 kN en een gelijkmatig verdeelde belasting van 10 kN/m2. Dit levert de volgende dekeigenschappen op:
Eigenschappen rijdek over 3m breedte
| h | b | EIy | GA |
| [mm] | [mm] | [kNm2] | [kN] |
| 150 | 3.000 | 13.555 | 250.773 |
Hierbij is rekening gehouden met een totale conversiefactor van 0,81 voor degradatie en droog/nat-klimaatomstandigheden volgens CUR 96. Met deze eigenschappen is de maximale verplaatsing 2,7 mm en een maximale spanning van 26 MPa bij 20 mm dikke flenzen.
DEKSEGMENT VAN 30 M
Het ontwerp is gebaseerd op een hart op hart afstand van 30 m tussen de kabels. De kabels zijn verbonden aan de stalen dwarsdragers. Op deze stalen dwarsdragers rusten de VVK deksegmenten. Het rijdek
wordt ondersteund door een VVK dwarsdrager; de VVK dwarsdragers worden weer ondersteund door VVK langsliggers. Een deksegment bestaat uit een rijdek zoals hiervoor omschreven. De langsliggers en
dwarsdragers worden uitgevoerd met een sandwichconstructie om knikken van de langsliggers en dwarsdragers te voorkomen. Om voldoende stijfheid en een goede aerodynamische vorm te verkrijgen, wordt de onderzijde afgedekt met een VVK sandwichplaat en worden de zijkanten afgerond. In de langsliggers kunnen openingen gemaakt worden, zodat het gehele deksegment van binnenuit is te inspecteren.
Elk deksegment is breed genoeg om twee rijstroken te dragen; echter voor de stabiliteit in dwarsrichting is een breder dek nodig. Als bovengrens wordt voor het bepalen van de afmetingen van het deksegment alleen de breedte van het asfalt (breedte 8 m) meegenomen. De belasting op het deksegment door verkeer bedraagt een puntlast 1.000 kN en gelijkmatig verdeelde belasting van 37,5 kN/m. Op basis van een ligger op twee steunpunten (bovengrens) worden de afmetingen gecontroleerd. De eigenschappen van het deksegment zijn:
Ook hier wordt een conversiefactor van 0,81 gebruikt. De maximale doorbuiging onder verkeer is 71 mm < 30.000/200 = 150 mm. De maximale spanning bij 20 mm dikke
flensen is 26 MPa.
Deksegment 30 m lang, 6 m breed
| h | b | EIy | GA |
| [mm] | [mm] | [MNm2] | [MN] |
| 2.250 | 6.000 | 20.447 | 1.057 |
HET GLOBALE DEK
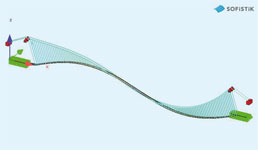
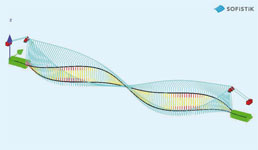
In deze haalbaarheidstudie is het dek niet geoptimaliseerd, omdat we vooral naar voren willen brengen wat de mogelijkheden van het materiaal zijn. De constructie zonder de pylonen is gemodelleerd in Sofistik en met behulp van de form-finding module zijn voor de permanente belastingen de momenten in het dek zo gelijk mogelijk verdeeld en verplaatsingen zodanig geoptimaliseerd dat het dek geen doorbuiging heeft onder de permanente belasting. In het Sofisik-model is het dek als een ligger geschematiseerd.
 STALEN DWARSDRAGER
STALEN DWARSDRAGER
Voor de verbinding tussen de twee dekken in dwarsrichting is een stalen dwarsdrager gebruikt. Door de ligger in staal uit te voeren denken we makkelijker de belangrijke verbindingen van de hoofddraagconstructies te kunnen uitvoeren. De dwarsdrager hangt tussen de twee hangkabels en is hier ook mee verbonden. Daarna worden de VVK dekken tussen de dwarsdragers gehangen.
Het ontwerp is zodanig uitgewerkt dat de dwarsdrager het VVK dek altijd verticaal ondersteunt. Het VVK dek wordt verder via een lijm- of een injectieverbinding aan elkaar gekoppeld. Als back-up worden er ook boutverbindingen aangebracht. Door openingen in het dek en de dwarsdrager, met een breedte van 2 m en een hoogte van 2 tot 3,5 m, kunnen de verbindingen die zijn aangebracht, worden geïnspecteerd. Op deze manier hebben we een robuust en betrouwbaar ontwerp gemaakt. De gehele constructie is verbonden met bewezen standaardverbindingen; de verbinding van VVK dek met de dwarsdrager is het meest spannend en zal ook getest moeten worden, maar heeft altijd een tweede draagweg, omdat het altijd verticaal ondersteund is en de verbinding met lijm en bouten is uitgevoerd.
HOOFDKABELS VAN DE HANGBRUG
Als een alternatief voor de stalen kabels kunnen koolstofkabels gebruikt worden voor grote bruggen. Deze koolstofkabels hebben echter wat nadelen: ze zijn niet makkelijk te verankeren en niet makkelijk te vervoeren. Wij hebben gekozen om Aramide kabels toe te passen van de firma FibreMax. Hiermee hebben we FibreMax uitgedaagd naar de mogelijkheden van deze grote overspanning. Zij hebben aangegeven dat, indien ze de ruimte en de opdracht hebben, ze deze kabels binnen twee jaar kunnen produceren. Nu heeft een Aramide kabel wel een nadeel:
deze is namelijk minder stijf (E = 129.000 MPa) dan een stalen kabel en zal daarom meer doorhangen. Dit zal gecompenseerd moeten worden. Door de vormgeving van de Aramide kabel zal de kabel in de exacte lengte geproduceerd moeten worden, aangezien beide kanten voorzien zijn van een ankerkop (zie figuur rechts). De totale hoofdkabel is opgebouwd uit meerdere kabels. De productie van de kabels is gebaseerd op “endless winding technology”. Deze techniek is een totaal automatisch proces van continu wikkelen van parallelle strengen van vezels rond twee eindbeëindiging/fittingen tot de gewenste kabelsterkte of kabelrek bereikt is. Nadat de lengte is geprogrammeerd, berekent de computer van de EWR (Endless Winding Robot) de hoeveelheid vezels en het aantal lussen die voor de gespecificeerde kabel benodigd zijn. Tijdens het wikkelproces zorgt de EWR voor gelijke spanning in alle vezels met een nauwkeurigheid van 0,1%.
Dit resulteert in de hoogste bezwijkbelasting en de kleinst mogelijke diameter. Het zorgt er ook voor dat de kabels met constante kwaliteit worden geproduceerd.
Het grootste deel van de kruipeffecten kunnen in het fabricageproces verdisconteerd worden.
De meest kritische ontwerpcriteria zijn:
• sterkte (treksterkte / MBL);
• toegepaste belastingen (min/max) tijdens de levensduur (en de frequentie van deze lasten);
• maximaal toegestane rek onder belasting;
• pengrootte;
• verwachte levensduur.
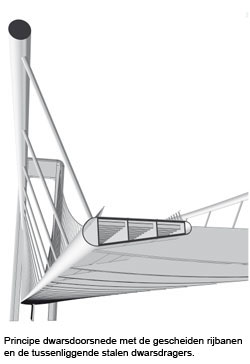 Alle vezels in de kabels zijn parallel gewikkeld. Dit is vergelijkbaar met het stalen parallel-wired kabelsysteem. Er is slechts elastische verlenging van het vezelmateriaal en daarmee vereist dit geen (of minder) voorspanning bij de installatie van de kabels. Uiteraard kunnen de kabels worden gespannen. De lengte van de kabels is geregeld binnen het geautomatiseerde productieproces en de lengte- toleranties kunnen tot een minimum worden beperkt (tot <1 mm, afhankelijk van de lengte van de kabel). Door het eindeloze wikkelproces wordt de eindsterkte (MBL) van de kabel bepaald in de eindafsluiting. Een FiberMax-kabel zal altijd breken in de beëindiging in een vooraf aangewezen gebied, aangezien de vezels hier in een lus lopen. Voor het ontwerp van de kabel is het eveneens belangrijk om het penformaat te kennen. De grootte van de pen heeft invloed op de maximale bezwijklast. De kabels zullen worden bevestigd aan de pyloon en dus worden de verschillende kabels (met een totale diameter van 2 m) verspreid op de pyloon.
Alle vezels in de kabels zijn parallel gewikkeld. Dit is vergelijkbaar met het stalen parallel-wired kabelsysteem. Er is slechts elastische verlenging van het vezelmateriaal en daarmee vereist dit geen (of minder) voorspanning bij de installatie van de kabels. Uiteraard kunnen de kabels worden gespannen. De lengte van de kabels is geregeld binnen het geautomatiseerde productieproces en de lengte- toleranties kunnen tot een minimum worden beperkt (tot <1 mm, afhankelijk van de lengte van de kabel). Door het eindeloze wikkelproces wordt de eindsterkte (MBL) van de kabel bepaald in de eindafsluiting. Een FiberMax-kabel zal altijd breken in de beëindiging in een vooraf aangewezen gebied, aangezien de vezels hier in een lus lopen. Voor het ontwerp van de kabel is het eveneens belangrijk om het penformaat te kennen. De grootte van de pen heeft invloed op de maximale bezwijklast. De kabels zullen worden bevestigd aan de pyloon en dus worden de verschillende kabels (met een totale diameter van 2 m) verspreid op de pyloon.
PYLOON
In ons ontwerp hebben we aangenomen dat de pyloon in beton wordt uitgevoerd. De pyloon staat zo dicht mogelijk aan, of net in het water om de bouw zo makkelijk mogelijk te houden.
RESULTATEN
Op basis van de eerdere handberekeningen en praktische keuzes zijn de afmetingen van het dek ingevoerd in het Sofistik-programma. Dit leidt tot de volgende resultaten.
DEKCONSTRUCTIE
| Structure BGT |
FRP-dek vertikaal |
FRP-dek horizontaal |
| Normaalkracht | 1.300 N | |
| Normaalspanning | 12,17 MPa | |
| Moment | 13.450 kNm | 64.600 kNm |
| Buigspanning s | 9,02 MPa | 11,34 MPa |

De totale maximale spanning in het dek is in dwarsrichting ongeveer:
12,17 + 11,34 = 23,51 MPa << 1,2% van 18.573 MPa x 0,81 / (1,15 x 1,5) = 129,2 MPa (Op basis van BGT is er een veiligheid van: 129,2 / 21,37 = 6,04). De berekening van de toegestane belasting is gebaseerd op de 1,2% rek van het materiaal aan de buitenkant van het dek (in dit geval de verticale lijven), vermenigvuldigd met de conversiefactor en gedeeld door de materiaalfactoren m1 en m2, overeenkomstig een update van CUR 96 die in ontwikkeling is. De huidige CUR 96 [6] wordt vervangen door een nieuwe CUR 96, gebaseerd op de principes van de Eurocode.
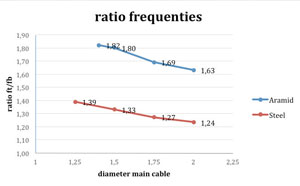
De verticale doorbuiging wordt gedomineerd door de stijfheid van de hoofdkabel en iets minder door de stijfheid van het dek in dit ontwerp. Voor de hoofdkabel hebben we een eerste berekening gemaakt en op basis van deze afmeting kwamen we uit op een diameter van 2 m. Daarna zijn we gaan optimaliseren en hebben we een vergelijk gemaakt met een stalen kabel. In onderstaande grafiek zijn de resultaten weergegeven: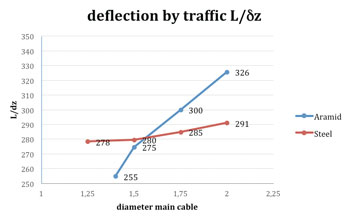
Met de Aramide kabel konden we tot een diameter van 1,4 m de Sofistik-som maken; daarna werd het model instabiel en zouden we de afstand van de dekken moeten vergroten. Bij de stalen kabel konden we tot een diameter van 1,25 m optimaliseren. Wat opvalt is dat de Aramide kabel tot ca. een diameter van 1,5 m minder doorbuigt dan de stalen kabel onder de verkeersbelasting. Verdere studie naar de optimale stijfheid van dek en kabel is nodig om tot een optimaal ontwerp te komen.
De stalen dwarsligger is niet in detail ontworpen, maar binnen de aangenomen afmetingen van de kokerconstructie kan deze verder worden gedetailleerd.
KABELS
Voor de hoofdkabel en de hangers is gekozen voor een Twaron 2200 (Aramide) kabel. In Sofistik zijn de maatgevende krachten bepaald voor de kabels.
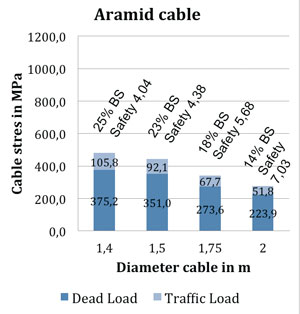
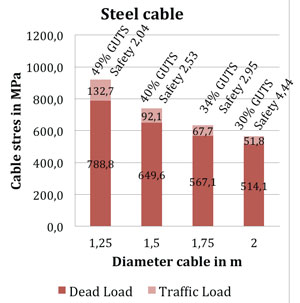
De maximale spanning die wordt toegestaan in deze fase is voor Aramide: 2.500 MPa /1,3 = 1.923 MPa. Voor stalen kabels geldt meestal een begrenzing van de spanning op 45% van de toelaatbare staalspanning en wordt uitgedrukt in GUTS. 45% GUTS wil zeggen dat het staal na 2 miljoen belastingcycli met een spanningsbereik van 200 MPa nog tot 45% van zijn toelaatbare spanning moet kunnen worden belast. Bij Aramide is niet zozeer de vermoeiing een probleem, maar meer de belasting onder hoge temperaturen. Uit testen is gebleken dat als men de Aramide kabel onder een constante temperatuur van 50°C houdt, je de kabel meer dan honderd jaar kan belasten tot 46% van zijn sterkte (Braking Strength (BS)), welke voor ons is aangehouden op 1.923 MPa, zoals hierboven is beschreven. Wat opvalt is dat de staalkabel met een diameter van 1,25 m boven de maximale 45% GUTS komt en daarmee niet meer voldoet. De veiligheid op deze stalen kabel is op dat moment nog maar 2,04. Voor de Aramide kabel zitten we bij een diameter van 1,4 m op 25% BS en ligt daarmee nog ver onder de 46%. De veiligheid van de Aramide kabel is in dit geval nog 4,04. Stel dat we over de volledige belasting (meeste belasting is echter permanent) een belastingfactor zetten van 1,65 (100 jaar levensduur) dan blijft er voor het materiaal nog een veiligheidsfactor van 2,44 over en dat lijkt voldoende.
Frequenties Aramide d=2,0 m
| Frequenties | Load Case-nummer |
Frequenties [Hertz] |
| Torsie | 2008 | 0,085 |
| Verticaal | 2003 | 0,052 |
| e = torsie/verticaal | 1,620 |
DYNAMISCH GEDRAG
De natuurlijke frequenties en bijbehorende trilvormen zijn bepaald voor de brugconstructie aan de hand van de BGT spanningstoestand.
Uit nevenstaande grafiek blijkt dat bij de Aramide kabel de frequenties verder uit elkaar liggen dan bij staal en dat een kleinere diameter gunstiger resultaten geeft.
Voor de Aramide kabel met een diameter van 2,0 m is de kritische windsnelheid bepaald. De eerste translatie- en torsiebelastingfrequenties zijn respectievelijk 0,052 en 0,085 Hz.
Om flutter van het dek te voorkomen, moeten de frequenties voldoende uit elkaar blijven. Volgens de aangepaste Selbergformule (zie bijvoorbeeld Banck & Almberg [4]) is de kritische windsnelheid afhankelijk van de verhouding van de translatie- en torsiebelastingsfrequentie. Met de huidige verhouding van 1,6 en de geometrie en traagheidseigenschappen van de brug, is de kritische windsnelheid 23 m/s, dat overeenkomt met 9 Beaufort en marginaal hoger is dan de Golden Gate Bridge [8]. Bij zulke hoge windsnelheden heeft turbulentie de neiging om flutter van het dek uit te sluiten; de berekende kritische windsnelheid lijkt daarom voor deze haalbaarheidsstudie voldoende. Maar nadere studie is nodig.
De vortex-excitatie van de hangers is onderzocht door het bepalen van het Scrutongetal. Het omslagpunt voor de gevoeligheid op vortex-excitatie ligt bij een waarde van 25, waarbij een lager getal leidt tot een grotere gevoeligheid. Het Scrutongetal wordt onder andere berekend door het logaritmisch decrement van de constructieve demping (ds), die zich met een materiaaldemping (?) verhoudt. Voor de berekening is in overleg met FibreMax uitgegaan van een logaritmisch decrement
van 0,03. Het berekende Scrutongetal van 55 geeft voldoende ongevoeligheid voor vortexexcitatie.
ARCHITECTONISCHE INVULLING
In de nieuwe E39 (1.100 km lang) zijn meer hangbruggen gepland. Een familie van bruggen, ontworpen door één architect, maakt de nieuwe E39 meer herkenbaar en ‘one of a kind’ in de wereld. Voor hangbruggen moet het architectonisch ontwerp het structurele ontwerp volgen. Maar VVK-materiaal van het brugdek is bekend om zijn vormvrijheid en vereenvoudigt het realiseren van aërodynamische en architectonische vormen. Uit architectonisch oogpunt ligt de ware schoonheid van deze brug in de afmetingen ervan.
Vrachtauto’s en gewone auto’s zijn op dit soort grote bruggen maar kleine stipjes, vangrails en borstweringen vallen nauwelijks op. De brug is ontworpen met gebogen dekken. Het dek kan door de VVK toepassing mooi aerodynamisch gestroomlijnd worden. Het belangrijkste aspect waarop een architect zich echt kan uitleven, zijn de pylonen. Verschillende pyloonconfiguraties zijn bekeken, zoals een pyloon tussen de dekken of twee losse pylonen aan beide zijden van de dekken en zelfs schuine pylonen. Echter om constructieve redenen zijn schuine pylonen weer snel vergeten. Bij het ontwerpen van een hangbrug van deze afmetingen veroorzaakt de zijwaartse wind grote krachten, waardoor, gecombineerd met de grote overspanning, voor de pylonen een stijf portaal met dwarsverbindingen nodig is. Zo krijgt het ontwerp een robuust uiterlijk met een zeer slank brugdek.
CONCLUSIE
In het begin van het artikel is aangegeven op welke vier onderdelen wij ons hebben geconcentreerd. Hier onder worden de conclusies van deze vier onderdelen gegeven.
1 Het eigen gewicht van het VVK dek is ongeveer 250-300 kg/m2 en is lichter (ca. 20 – 30%) dan stalen dekken voor hangbruggen. De hoofdkabel in Aramide zorgt voor reductie van ca. 75% van het eigen gewicht ten opzichte van traditionele stalen kabels. Optimalisatie laat zien, dat een kabel van 1,4 m toegepast kan worden in plaats van 2,0 m.
2 Bij een diameter van 1,4 m voor de Aramide hoofdkabel is de doorbuiging ca. 14,52 m wat overeenkomt met L/255. Hoewel in [5] is aangegeven dat L/200 acceptabel is, zouden we toch aanbevelen om meer richting de L/300 te gaan en dek en kabel iets stijver uit te voeren.
3 De spanningen in het VVK dek en de Aramide kabels zijn voldoende laag en hebben voldoende veiligheid.
4 De verhouding tussen de verticale belastingfrequenties en de torsiebelastingfrequenties is 1,62 bij een diameter van 2,0 m. Dit geeft een kritische windsnelheid van 23 m/s, dat overeenkomt met 9 Beaufort.
Uit de studie blijkt dat bruggen met grote overspanningen ontworpen kunnen worden met nieuwe lichtere materialen zoals VVK. Het dek en de kabels voldoen aan hun functies en de spanningen zijn lager dan voor staalconstructies, wat positief is voor de vermoeiing en maakt verdere optimalisatie mogelijk. De lage onderhoudskosten voor dit soort bruggen gebouwd met VVKmaterialen, is een heel groot voordeel. Denk je maar eens in dat je een stalen dek van 3.700 m overspanning moet gaan schilderen, met alles wat erbij komt kijken, terwijl je weet dat je dat niet het hele jaar kunt doen! VVK is al een bewezen materiaal voor brugdekken voor hoofdoverspanningen tot 30 m; grotere overspanningen zijn mogelijk, maar zijn nog niet gerealiseerd. De Aramide kabels zijn al voor zwaar belaste constructies, zoals grote kranen, toegepast, maar nog niet op deze schaal. Dit artikel toont aan dat de realisatie van dit soort bruggen met VVK en Aramide mogelijk is. Meer gedetailleerde berekeningen en tests zijn nodig om het verder optimaliseren van het ontwerp mogelijk te maken.
VERANTWOORDING
De auteur is dank verschuldigd aan de overige medewerkers aan dit onderzoek, te weten: Liesbeth Tromp, Joris Smits, Alex Swart, Sander Meijers, Peter Hagenaars en Michel Kortenaar van Royal HaskoningDHV, Jaco Reusink van Gemeente Werken Rotterdam en aan het overleg met FibreMax.
LITERATUURVERWIJZING
1 Chen W., Duan l. Bridge engineering handbook, second edition, Fundamentals, CRC press, Taylor and Francis Group; 2014.
2 Lewis W. J. Smith L. A Mathematical Model for Assessment of Material Requirements for Cable Supported Bridges: Implications for Conceptual Design. Warwick: University of Warwick; 2012.
3 Keller T., Use of FRP in Bridge Construction, Structural engineering documents 7, Zurich: IABSE-AIPC-IVBH; 2003
4 F. Banck, O.R. Almberg, Application of CFRP cables in super long span cable supported bridges, a feasibility study, Master’s thesis, Chalmers University of Technology, 2014
5 Statenes vegvesen, Sognefjorden Feasibility Study of Floating Bridge, 11258-03 Main report; 2013
6 CUR COMMISSION C124, “Recommendation 96 “ Fibre-Reinforced Polymers in Civil Load-Bearing Structures”, CUR Gouda, 2003.
7 Teijin, Static loading of Twaron and Technora, QBT 41303.1.1, Arnhem, The Netherlands, 2010
8 E. Simu, R.H. Scanlan Wind effects on structures, Fundamentals and Applications to design, John Wiley & Sons, inc. New York, United States of America,1996.