Dr. Ing. A. Romeijn

Brugtrillingen veroorzaakt door dynamische belastingen

Bij bruggen bestaat de trend om steeds slanker te willen construeren. Overspanningen nemen toe, het aandeel van eigengewicht neemt ten opzichte van de nuttige belasting af en er worden steeds vaker andere (minder zware) materialen gebruikt zoals aluminium, stalen kabels en vezelversterkte kunststoffen. Een voorbeeld hiervan is de Millennium Bridge in Londen.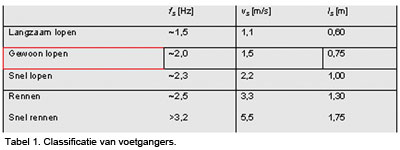
Het toepassen van zowel staal als beton met een hogere sterkte in combinatie met moderne verbindingstechnieken brengt met zich mee dat minder materiaal nodig is. De consequentie hiervan is dat de eigenfrequentie inclusief de demping van de brug afneemt waardoor de brug meer gevoelig is voor bewegen onder dynamische belasting. Deze gevoeligheid geldt in het bijzonder wanneer de eigenfrequentie van de gehele brug samenvalt met de frequentie van de belasting ten gevolge van bijvoorbeeld verkeer (voetgangers, treinen, enz.) en wind. Dat geldt ook voor onderdelen van de brug, waarvan de eigenfrequenties samenvallen met die van de belastingen op die onderdelen.
Gekeken naar het brede spectrum van verkeer zijn voetgangersbruggen en fietsbruggen verhoudingsgewijs het meest vatbaar voor trillingen, dan volgen spoorbruggen en op de laatste plaats verkeersbruggen. Voor alle bruggen geldt verder dat er specifieke onderdelen van de brug, bijvoorbeeld de hangers bij een boogbrug en de kabels bij een tuibrug, trillingsgevoelig kunnen zijn. Zo zien we dat er extra voorzieningen nodig waren bij de in de afgelopen 15 jaar gebouwde bruggen; onder andere de spoorbrug over de A12 bij Nootdorp; de Erasmusbrug in Rotterdam en de Werkspoorbrug in Utrecht. Waarom staan verkeersbruggen op de laatste plaats? Wel, het belastingbeeld is sterk wisselend van karakter: vrachtverkeer, personenwagens, er is een breed scala aan lastenstelsels en de rijsnelheid is vergeleken met treinverkeer laag. Dit alles wil niet zeggen dat bruggen voor wegverkeer niet trillingsgevoelig kunnen zijn.
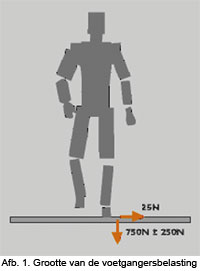
Bij het ontwerp van een brug wordt vaak op een indirecte manier met trillinggevoeligheid omgegaan. Dat wil zeggen dat er een toelaatbare vervorming als uitgangspunt wordt gehanteerd. Hiermee zijn we gelijk in een ‘gevarenzone’ beland, want een eenduidig antwoord op wat toelaatbaar is, is met name voor verkeersbruggen niet mogelijk. Dit verklaart bijvoorbeeld dat bij een aanbiedingsontwerp de betrokken concurrerende partijen een verschillend uitgangspunt hanteren en dus met totaal verschillende oplossingen en dus ook verschillende investeringsbedragen voor de dag komen. Zo zou het kunnen gebeuren dat voor het ontwerp van een tuibrug het ene ontwerpbureau uitgaat van een toelaatbare doorbuiging van 1/300 van de overspanning en een ander van 1/500 van de overspanning. Een dergelijk verschil kan allesbepalend zijn voor het eindresultaat. Toch zou gelet op de informatie, die opgenomen is in de brugspecifieke normen deze ‘vrije’ interpretatie niet mogen plaatsvinden.
Een scala aan factoren laat zich uiteindelijk vertalen in stijfheidseisen voor bijvoorbeeld de doorbuiging en hoekverdraaiing. Aanvullend is soms een dynamische analyse nodig. Hiermee wordt inzicht verkregen in het trillingsgedrag van de brug en daarmee kan een uitspraak worden gedaan over optredende versnellingen die een maat zijn voor het comfort van de reizigers in over de brug rijdende voertuigen. Bij het ontwerp van de Moerdijkbrug in de nieuwe hoge snelheidslijn zijn aan dit comfort zeer hoge eisen gesteld. Trillingen vormen over het algemeen een risico voor de duurzaamheid van een brug maar hebben hoofdzakelijk betrekking op het comfortgedrag.
Vooral voetgangersbruggen zijn vatbaar voor trillingen. Het is vrij lastig om een slanke voetgangersbrug te ontwerpen zonder dat de eigenfrequenties samenvallen met het brede frequentiespectrum van voetgangers. Vaak wordt dan ook vanaf het begin rekening gehouden met voorzieningen voor eventuele extra demping.
Dit artikel beperkt zich tot voetgangersbruggen. In een te zijner tijd op te nemen vervolgartikel zal op het dynamisch gedrag van respectievelijk spoorbruggen en verkeersbruggen worden ingegaan.

Dynamisch gedrag van voetgangersbruggen

De belasting veroorzaakt door een voetganger is variabel in de tijd. Verschillende voorschriften geven tekst en uitleg over deze belasting, hoewel deze informatie vaak niet compleet is. Het lastige is namelijk dat een voetganger naast langzaam, gewoon of snel lopen, ook kan rennen, springen, enz. De meeste voorschriften hebben alleen het loopgedrag opgenomen.
Een overzicht van de verschillende mogelijkheden van frequenties is opgenomen in tabel 1.
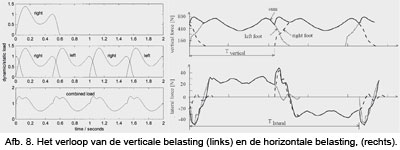
De eerste kolom geeft een opdeling in snelheid van verplaatsen en de tweede kolom geeft de bijbehorende frequentie. Bijvoorbeeld in geval van gewoon lopen raakt elke 0.5 sec (fs = 2,0 Hz) een voet het wegdek. Een verschijnsel bij het lopen is dat de belasting niet zuiver verticaal gericht is maar tevens een component in dwarsrichting kent, zie afbeelding 1. De verticale belasting werkt uiteraard in dezelfde richting maar in dwarsrichting wisselt deze telkens van teken. Daarom is de belastingfrequentie in dwarsrichting 50% van die in verticale richting. De derde kolom geeft de snelheid van verplaatsen weer en de laatste kolom de stapgrootte.

Het verband tussen verplaatsing, snelheid en versnelling is opgenomen in tabel 2.
Zoals aangegeven in afbeelding 1 is de verticale belasting gemiddeld 750 N en de zijdelingse belasting 25 N (altijd naar buiten gericht).
Ons loopgedrag heeft niet zo snel de neiging zich aan te passen aan het verticaal bewegen van de brug. Voor horizontaal bewegen van de brug ligt dit totaal anders. Dan hebben we de sterke neiging de loopsnelheid te laten synchroniseren met de frequentie van het zijdelings bewegen van de brug. Bij onvoldoende demping van de brug kan daardoor een grote zijdelingse verplaatsing van de brug optreden. Dit wordt nog versterkt met het gegeven dat bij grotere zijdelingse verplaatsing de beide benen meer uit elkaar worden geplaatst en daardoor neemt de zijdelingse belasting ook toe. Het belastingbeeld wordt nog complexer als het groepseffect wordt mee genomen. Bijvoorbeeld, hoe meer voetgangers per m2, hoe minder de individuele vrijheid van loopsnelheid en stapgrootte bestaat waardoor een steeds grotere neiging tot synchronisatie met het bewegingsgedrag van de brug optreedt. Ook deze vorm van synchronisatie is in het bijzonder van toepassing bij het zijdelings bewegen van de brug.
Het voorgaande laat zien dat een voetgangersbrug dynamisch wordt belast in zowel verticale als in dwarsrichting en dat deze belasting zich in de lengterichting van de brug verplaatst. De gemiddelde frequentie bedraagt 1.4 – 2.4 Hz voor de verticale belasting en 0.7 – 1.2 Hz voor de horizontale belasting, zie afbeelding 2. Het venijn bij ontwerp van voetgangersbruggen is dat de eigenfrequentie van de brug vaak in het frequentie gebied van de voetganger valt. Dit verklaart de regelmatig terugkerende problemen rondom dynamisch gedrag van dergelijke bruggen. Gemakshalve wordt vaak een ondergrens van 4 Hz als ontwerpeis gehanteerd.

Rekentechnische beschouwing van dynamisch gedrag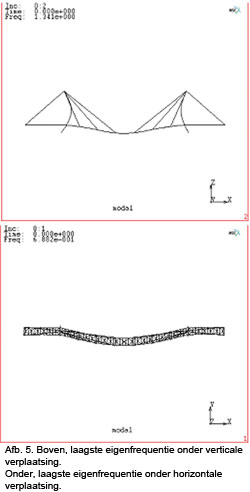

Voor het ontwerp van bruggen onder dynamische belasting bestaan globaal gezegd twee rekenmethoden:
• eigenwaarde analyse; berekening van de eigen-frequentie van de brug en toetsen of deze binnen de frequentie van lopen valt. De algemene uitdrukking voor de eerste eigenwaarde (buigfrequentie) conform Rayleigh’s methode is

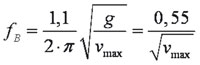
met v_max gelijk aan de verticale verplaatsing veroorzaakt door het eigengewicht van de constructie.

• transient analyse; hierbij wordt de rijvloer belast door een tijdsafhankelijke dynamische voetgangersbelasting. De berekende versnelling wordt getoetst op minimaal benodigd comfortgedrag.

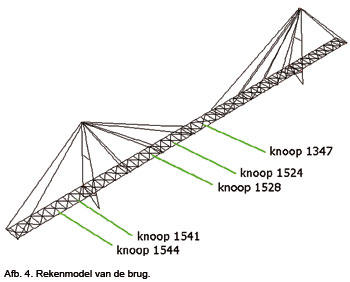
De betekenis van de twee methoden wordt voor een houten tuibrug gebouwd in Kerkrade nader toegelicht, zie de afbeeldingen 3 en 4. [1].

Eigenwaarde analyse
Enkele resultaten staan gegeven in afbeelding 5. Voor het bewegingsgedrag van de brug in horizontale richting geldt de eis:

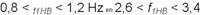
En voor de verticale richting geldt:

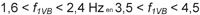
Wanneer nu de laagste eigenfrequentie buiten deze gebieden valt voldoet de brug aan de eis met betrekking tot comfort. Omdat demping karakteristieken van de brug volledig buiten beschouwing blijven is deze rekenmethode vrij conservatief van karakter. Dit  geldt in het bijzonder voor houten bruggen omdat dergelijke bruggen vaak veel gunstigere demping eigenschappen bezitten dan bijvoorbeeld stalen bruggen. Met andere woorden het niet voldoen aan het
gewenste frequentiebereik wil niet zeggen dat daarmee het ontwerp onjuist is, vooral als het een houten brug aangaat. Uiteraard kan extra demping aan de brug worden toegevoegd, daarover later meer.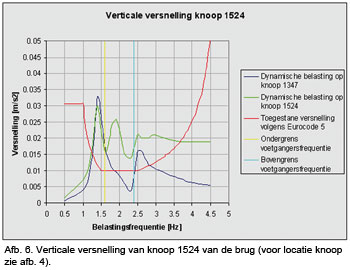
Transient analyse
Een dergelijke dynamische berekening is veel realistischer dan een eigenwaarde analyse. Het nadeel echter is dat het veel meer tijd en kunde vergt. De voetgangersbelasting gegeven in de Eurocode 5 over houten bruggen, ENV 1995-2, is gelijk aan

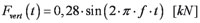
Afbeelding 6 geeft de verticale versnelling voor knoop 1524 en afbeelding 7 de horizontale versnelling voor knoop 1347. De versnelling is gegeven voor een range aan voetgangers frequenties.

De maximaal toelaatbare verticale versnelling, gegeven in de Eurocode, is gelijk aan

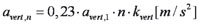
, zie de rode lijn in afbeelding 6.
De maximaal toelaatbare horizontale versnelling is gelijk aan

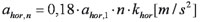
, zie de rode lijn in afbeelding 7.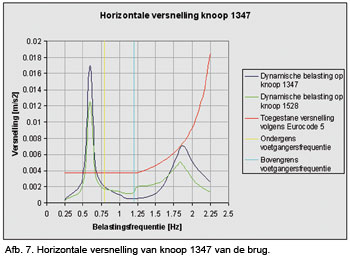
Een toelichting op deze laatste twee gegeven formules is verderop in dit artikel te vinden.
Een lastig aspect is het in rekening brengen van een waarde voor de inherente demping, de zogenoemde ?- waarde. Naast het materiaal zelf, hout - beton - staal, enz., spelen hierbij zaken als speling in de boutgaten, contactwrijving, enz.
Voor lage ζ- waarden, hetgeen het geval is voor brugconstructies, is de inherente demping ζ gelijk aan de logaritmische demping δ gedeeld door 2p. Conform de Eurocode geldt als indicatie
• staal δ = 0.03
• aluminium δ = 0.02
• beton δ = 0.05
• hout δ = 0.06 – 0.12 (afhankelijk van het soort van verbindingen)

Deze getallen moeten met een zekere voorzichtigheid worden gehanteerd omdat praktijkmetingen laten zien dat de demping van een brug aanzienlijk lager kan zijn en daarmee is de amplitude van bewegen groter en dus ook de versnelling.

Ontwerpcriteria voor voetgangersbruggen

Het verloop van de verticale belasting is toegelicht in afbeelding 8. De belasting bestaat uit een statische component, het gewicht van een persoon, plus een periodiek variërende component. Het geheel laat zich vertalen in een Fourier reeks:

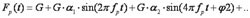
waarbij
G = het gemiddelde gewicht van een persoon
t = tijd
fp = loopfrequentie
an = dynamische vergrotingsfactor (DLF)
Fn = phase verschil

Gewoonlijk kan worden volstaan met de eerste drie termen waarbij de waarde voor DLF te vinden is in tabel 3.

Synchronisatie

Een natuurlijk gegeven is dat mensen de neiging hebben tot “in de pas” lopen. Dit kan betrekking hebben op aanpassen aan het loopgedrag van anderen, het zogenoemde groepseffect, en aanpassen aan de beweging van de brug zelf. Met andere woorden er is sprake van een zekere mate van synchronisatie en daarmee dus een versterking van dynamische belasting.

Groepseffect

Uit verschillende metingen is het effect van synchronisatie als gevolg van groepseffect onderzocht. Gebleken is dat de gemiddelde loopfrequentie hetzelfde blijft (2 Hz) met een standaardafwijking van 0.173 Hz, zie afbeelding 9. Met andere woorden als de loopfrequentie de 2 Hz nadert is de kans op synchronisatie tussen de voetgangers het grootst. Dit alles is in sterke mate afhankelijk van het aantal voetgangers per m2 (uitgedrukt als q-waarde).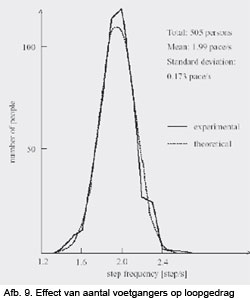
Wanneer q < 0.3, zullen alle voetgangers ongestoord van elkaar lopen. Voor q = 1.0, is het loopgedrag afhankelijk van anderen en dus gaat het naar de ca. 2 Hz. Bij q = 0.6 begint reeds een zekere mate van synchronisatie op te treden.

Bewegen van de brug

Een bepaald percentage van voetgangers heeft de neiging de loopsnelheid aan te passen aan de bewegingssnelheid van de brug. Ook dit is een vorm van synchronisatie. Afbeelding 10 laat zien dat naarmate de versnelling van bewegen toeneemt de neiging tot synchronisatie ook toeneemt.

Bijvoorbeeld bij een toelaatbare versnelling van 0.7 ms2 is het percentage voetgangers dat gaat synchroniseren gelijk aan 23%.
Het verschijnsel van synchronisatie brengt met zich mee dat een correctiefactor meegenomen moet worden. In feite komt het erop neer dat er berekeningen worden uitgevoerd waarbij slechts één voetganger wordt beschouwd. Vervolgens wordt op de gevonden resultaten een correctie uitgevoerd. De correctieformule is gelijk aan

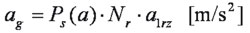
waarbij Ps(a) volgt uit afbeelding 10 en Nr = N·K , dit staat voor een equivalent aantal voetgangers waarbij N gelijk is aan het totaal aantal mogelijke voetgangers op de brug (dit is genormeerd) en K is een reductiefactor waarmee de synchronisatie veroorzaakt door groepseffect wordt meegenomen.

Wat zeggen de brugspecifieke normen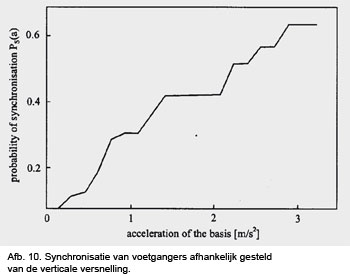

Eurocode EN 1990
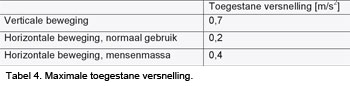
Het voetgangerscomfort moet zijn getoetst in de bruikbaarheidsgrenstoestand en wordt uitgedrukt in een toelaatbare versnelling, zie tabel 4.

Bij het bepalen van de versnelling van de brug moet het eigengewicht alsmede de permanente belasting worden meegenomen. Voor de stijfheid van de constructie moet gerekend worden met een belasting van korte duur, dat wil zeggen geen gereduceerde E-waarde van het beton als gevolg van kruipgedrag.
Er zijn drie verschillende dynamische belastingmodellen geformuleerd:
DLM1 er wordt uitgegaan van één voetganger
DLM2 er wordt uitgegaan van een groep voetgangers
DLM3 er wordt uitgegaan van een constante stroom van voetgangers.

Het is aan de ontwerper om te bepalen met welk model het ontwerp wordt uitgevoerd.
De eerste twee worden nader toegelicht.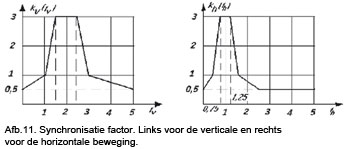
DLM1
De in rekening te brengen belastingen zijn gelijk aan:
• verticale component: Q_pv = 280 sin (2πgf_v . t) [N]
• horizontale component: Q_ph = 70 sin (2πgf_h . t) [N]
met
f_v = de frequentie van de brug bij verticale verplaat- sing, het dichtst gelegen bij de 2 Hz
f_h = de frequentie van de brug bij horizontale ver- plaatsing, het dichtst gelegen bij de 1 Hz.
DLM2
Dit model neemt het gedrag van een groep voetgangers in rekening.
De in rekening te brengen belastingen zijn:
• verticale component:
Q_gv = 280 sin . k_v (f_v) . sin (2πgf_v . t) [N]
• horizontale component:
Q_gh = 70 . k_h (f_h) . sin (2πgf_h . t) [N]

Voor f_v en f_h zie informatie gegeven bij DLM1. De waarden voor k_v (f_v) en k_h (f_h) staan gegeven in afbeelding 11.

Eurocode 1995-2
Deze norm gaat specifiek in op het ontwerp van houten bruggen. De toelaatbare versnellingen zijn gelijk aan tabel 4. Het comfort criterium moet worden getoetst indien voor de verticale beweging de brugfrequentie lager is dan 5 Hz en voor de horizontale beweging lager dan 2.5 Hz.

Verticale beweging
Voor één persoon moet de versnelling a_vert,1 in m/s² gelijk worden gesteld aan:

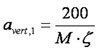	voor fvert = 2,5 Hz en
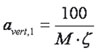	voor 2,5 Hz < fvert = 5,0 Hz

waarin
M = de totale massa van de brug in kg
ζ = de demping ratio

Ingeval van meerdere personen op de brug volgt de versnelling a_vert,n in m/s² uit
a_vert,n = 0,23 . a_vert,1 . n . k_vert
waarin
n = aantal voetgangers
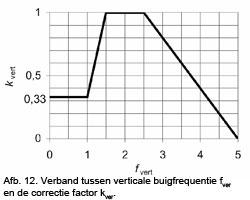
k_vert = correctie coëfficiënt volgens afbeelding 12

Het aantal voetgangers, n, moet gelijk worden genomen aan
n = 13 als sprake is van een groep van voetgangers
n = 0.6A ingeval van een continue stroom van voetgangers, waarbij A is het rijvloeroppervlak in m2.
De factor 0,23 volgt uit afbeelding 10 (vertical as P_s(a) ).
Als het gaat om rennende mensen over de brug dan geldt voor de verticale acceleratie

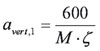voor 2,5 Hz < fvert = 3,5 Hz

Horizontale beweging
Voor één persoon moet de versnelling a_hor,1 in m/s² gelijk worden gesteld aan:

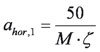voor 0,5 Hz < fhor = 2,5 Hz

Ingeval van meerdere personen op de brug volgt de versnelling
a_hor,n in m/s² uit a_hor,n = 0,18 . a_hor,1 . n . k_hor
waarin
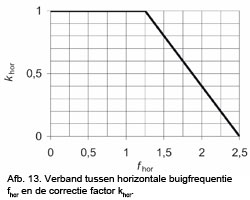
k_hor = correctie coëfficiënt volgens afbeelding 13
n = aantal voetgangers (dit wordt op dezelfde wijze bepaald als hierboven beschreven onder verticale beweging.

Voorbeeld: London Millennium bridge

www.arup.com/milleniumbridge
Een voorbeeld van een voetgangersbrug die sterk aan trillingen onderhevig was, is de Londen Millennium Bridge. De brug heeft een lengte van meer dan 300 m met drie overspanningen waarvan de langste 144 m, zie afbeelding 14. Om esthetische redenen is een hangkabel toegepast met een pijl van slechts 2.3 m, 6 maal minder dan bij een klassieke hangbrug.

Veroorzaakt door die geringe pijlmaat bedraagt de trekkracht in de kabel circa 20.000 kN. Dit ondanks het lage eigengewicht van de brug, 2 ton per m1. De kabel is opgebouwd uit vier 120 mm diameter locked coil kabels die verankerd zijn aan de landhoofden, zie afbeelding 15.

De rijvloer is opgebouwd uit geprefabriceerde elementen met een lengte van 8 m. De breedte is gelijk aan de totaal benodige breedte van 4 m. Het dek is opgebouwd uit aluminium extrusieprofielen. Het geheel is via uitkragende liggers aan de kabels opgehangen. De uitkragende liggers bestaan uit een kokerprofiel met een verlopende hoogte van 450 mm tot 225 mm. Aan de randen van het dek is een buisprofiel geplaatst. Dit profiel is de doorgaande ondersteunende ligger voor de rijvloer. Enkele details van de rijvloer staan gegeven in afbeelding 16 .

Op de openingsdag van de brug, juni 2000, ging het gelijk al fout. De brug begon veroorzaakt door de voetgangers, in dwarsrichting hevig te slingeren. Voor de zijoverspanning bedroeg de bewegingsamplitude 50 mm bij 0.8 Hz. Voor de hoofdoverspanning bedroeg deze respectievelijk 75 mm bij 1.0 Hz. Dergelijke bewegingen kunnen tot groot aantal slachtoffers leiden, zelf met fatale afloop. Een paar dagen na de openingsdag is de brug gesloten voor nader onderzoek.

Oplossing van het probleem
De oplossing kan worden gevonden door het nemen van de volgende maatregelen.

Toename van de brugstijfheid
Een mogelijke oplossing zou kunnen zijn om de stijfheid van de brug te vergroten, zodat daarmee de eigenfrequentie toeneemt en buiten het gestelde gebied valt. Theoretisch geldt dat om de eigenfrequentie met een factor twee te verhogen de stijfheid met een factor 4 moet toenemen. Echter, doordat de massa daarmee toeneemt is weer een extra verhoogde stijfheid noodzakelijk. Kortom, dit bleek geen haalbare oplossing te zijn omdat daarmee de brug een totaal andere gedaante krijgt.

Toename van de demping
Er bestaan verschillende technieken om de demping van een brugconstructie te laten toenemen.
Bijvoorbeeld bij kleine amplitudes kan gewerkt worden met materiaal demping vanuit visko-elastisch gedrag van het materiaal zelf. Bij grote(re) amplitudes werkt deze methode niet goed en moet eerder gedacht worden aan massa dempers.
Een overzicht van demping systemen:

	tuned mass demper (TMD); zijn geschikt voor een specifiek frequentiegebied. Het is een passieve demping, een zogenoemd massa-veer systeem. Met andere woorden de grootte van de massa en de stijfheid van de veer wordt zodanig ontworpen dat dit geheel in tegenfase gaat trillen;
	tuned liquid demper (LTD); een verhoudingsgewijs goedkope oplossing en eenvoudig te installeren. In de meest eenvoudige vorm kan hierbij gedacht worden aan een gesloten bak met daarin opgenomen water
	viskeuze demper; deze zijn geschikt voor een breed spectrum van frequenties. Veelal wordt hierbij een cilinder gevuld met silicone vloeistof toegepast. De demper moet wel aan een vast onderdeel, bijvoorbeeld aan een pijlerconstructie zijn verbonden.

Uiteindelijk is de oplossing gevonden in het toepassen van 37 viskeuze dempers in combinatie met 50 TMD’s. Een extra staalconstructie is aan de onderzijde van de rijvloer geplaatst. Het betreft hierbij verbandstaven met aan de uiteinden daarvan opgenomen de viskeuze dempers, zie afbeelding 17. Het zijdelings bewegen van de brug wordt door deze verbanden beperkt en de energie in deze verbandstaven wordt door deze dempers geabsorbeerd.

De demping van de brug is hiermee toegenomen van 0.5% naar 20% en daarmee is de versnelling van bewegen met een factor 40 afgenomen.

Literatuur

[1] Ir. J. van der Asdonk, Master thesis “Voorontwerp en dynamische analyse van een hardhouten tuibrug voor langzaam verkeer”. TU Delft jan. 2006.
[2] Msc F. Haukson, Master thesis “Dynamic behaviour of footbridges subjected to pedestrian-induced vibrations”. ISSN 0281-6679.
[3] T. Fitzpatrick, et al. Linking London: The Millennium Bridge. Royal Academy of Engineering.
[4] R.L. Pimental, et al. Evaluation of design requirements for footbridges excited by vertical forces from walking. Can. J. Civ. Eng. 28: 769-777 (2001).

Download hier het artikel in pdf-formaat