A.J. Persoon

Inleiding

In het begin van de jaren 80 is, als alternatief voor een tunnel onder de Westerschelde, in opdracht van de stichting Westerschelde Oever Verbinding (W.O.V), het ontwerp van een hangbrug onderzocht in de lagesnelheidwindtunnels van het Nationaal Lucht- en Ruimtevaartlaboratorium. De beoogde brug, onderdeel van de oeververbinding, zou met een vrije overspanning van 918 m en pylonen van 92 m hoogte, één van de grotere hangbruggen in Europa zijn geworden.
Sedert 1970 wordt op het NLR met regelmaat onderzoek verricht naar het trillingsgedrag van nieuw te bouwen verkeersbruggen. Doordat een brugdek als een slanke vliegtuigvleugel kan worden beschouwd, kan de bij het NLR aanwezige (aëro-elastische) rekenprogrammatuur worden toegepast. Zo kunnen de stabiliteit van een brugdek tegen ongewenst trillingsgedrag (flutter) en de responsie op wervelexcitatie door de wind worden voorspeld. Daarnaast wordt met schaalmodellen in de windtunnel gewerkt. De procedures waarop het windtunnelonderzoek is gebaseerd, komen overeen met die welke zijn ontwikkeld in de Verenigde Staten na het instorten van de Tacoma Narrows brug op 7 november 1940.
Bij het construeren van moderne verkeersbruggen speelt de wind een belangrijke rol.
Reden daarvan is dat, door nieuwe berekening- en constructietechnieken, verkeersbruggen kunnen worden voorzien van een lange vrije overspanning met een relatief laag eigen gewicht, die echter gevoeliger zijn voor trillingen.
Wordt de brug in staal uitgevoerd, dan zal ook de con-structiedemping laag zijn. Is daarnaast de geometrie van het brugdek verre van gestroomlijnd (zoals bij de voorgestelde hangbrug), dan zijn dit dé factoren die een windtunnelonderzoek rechtvaardigen. Om deze redenen is destijds dan ook aan het trillingsgedrag van de hangbrug over de Westerschelde, onder invloed van wind, de nodige aandacht besteed.
In deze bijdrage wordt nader ingegaan op het aërodynamisch onderzoek in 1981 verricht op het Nationaal Lucht- en Ruimtevaartlaboratorium.

Oorzaken van door wind opgewekte trillingen

Globaal genomen zijn er twee oorzaken aan te wijzen waardoor een verkeersbrug met een lange vrije overspanning in trilling kan geraken: wervelexcitatie en flutter [Lit.1].
a) “wervel - excitatie”
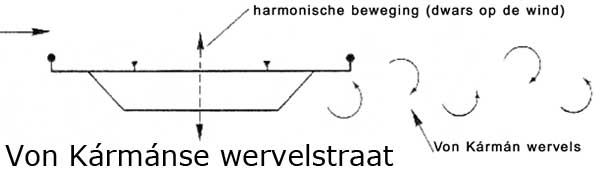
Hierbij is het brugdek door zijn vormgeving (zoals scherpe randen) in staat een (Von-Kármánse) wervelstraat te genereren. Trillingen ontstaan als de frequentie waarmee de wervels loslaten, samenvalt met een eigenfrequentie van de brug. Kenmerkend voor dit verschijnsel is dat het optreedt bij één specifieke windsnelheid omdat de wervelfrequentie (f) evenredig is met de windsnelheid (V). Voor het karakteristieke getal van Strouhal (S) geldt: S = f . D / V, waarin D de hoogte (m) van het brugdek voorstelt. De waarde van S bedraagt voor de meeste brugdekvormen S = 0,1 á 0,15.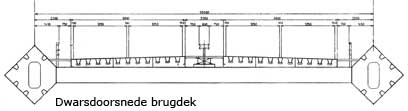

Wervel-excitatie doet zich meestal voor in een trillingsvorm met de laagste eigenfrequentie. Is deze frequentie bekend uit berekeningen, dan is ook de windsnelheid te schatten waarbij dit verschijnsel zich in de praktijk zal voordoen. Vaak blijkt deze lager te zijn dan V = 15 m/s (windkracht 6 à 7). Wervel-excitatie komt dan ook regelmatig voor. De responsie van een brugdek op wer-velexcitatie kan in een windtunnel op relatief eenvoudige wijze worden vastgesteld en worden getoetst aan de normen geldend voor passanten.
b) “Flutter”
Het brugdek wordt instabiel onder invloed van wind als twee trillingsvormen onder invloed van de luchtkrachten (aërodynamica) met elkaar gaan koppelen. Hierbij wordt door de wind arbeid geleverd in één van beide trillingsvormen, meestal de laagste torsietrillingsvorm. De demping zal door een onderlinge faserelatie afnemen, waardoor de trillingsamplitude in die trillingsvorm toeneemt. Boven een zekere windsnelheid zal de demping negatief worden. Het brugdek is dus niet meer gedempt en de amplitude wordt dermate groot dat breuk volgt. Dit verschijnsel is bekend uit de vliegtuigbouw, waar het “flutter “ wordt genoemd. In de civiele sector spreekt men van “brugdek flutter” en dat moet worden voorkomen.

Onderzoek in de windtunnel (1981)

Onderzocht zijn de windinvloeden op het brugdek en de pyloon.
a) Brugdek
Gezien de specifieke vormgeving van het brugdek (de beide kokerprofielen) is met name aandacht besteed aan het fluttergedrag [Lit.2]. Uit de literatuur is bekend dat de luchtkrachten van weinig gestroomlijnde brugdekvormen de theoretisch berekende fluttersnelheid van de constructie aanzienlijk zullen verlagen. Voor het flutteronderzoek is een model van een sectie van de brug gebruikt.
Het houten, maar starre, brugdekmodel (1100 mm leng-te) was in de windtunnel opgesteld tussen twee eindschotten waardoor de vereiste twee-dimensionale stroming rondom het model was gewaarborgd. Het model was bevestigd op drie elektrodynamische excitatoren, elk voorzien van een één-component rekstrookbalans waarmee de liftkracht werd gemeten. De excitatoren konden zowel in fase als in amplitude worden geregeld, zodat een zuivere slagtrilling (translatie) of een zuivere rotatie om de lengte-as (halfkoordepunt) van het model mogelijk was. Beide bewegingen zijn noodzakelijk om de luchtkrachten voor een flutterberekening te genereren. Het model was uitgerust met versnellingsmeters om de amplitude van de model trilling, zonder en met wind, op een zelfde wijze in te stellen. Na meting van de luchtkrachten bij een aantal windsnelheden en aandrijffrequenties van het model in de windtunnel, zijn flutterberekeningen uitgevoerd.

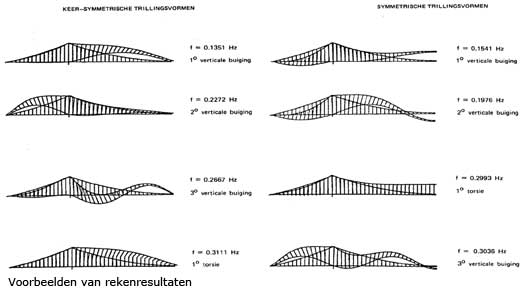
Daarvoor moesten eerst de eigenfrequenties en trillings-ormen van de brug bekend zijn. Deze zijn bepaald met een eindige-elementenmethode (destijds het programma “Trilstaaf” van het NLR). Voorbeelden van rekenresultaten zijn weergegeven in onderstaande figuur.
Vervolgens zijn met deze gegevens flutterberekeningen gemaakt met theoretische luchtkrachten geldend voor een oneindig dunne vlakke plaat. De resultaten kunnen een indicatie geven of de windsnelheid waarboven flutter kan optreden niet te laag is. Een windsnelheid > 40 m/s (als 10 minuten gemiddelde) wordt volgens de normen in ons land als een mimimum beschouwd.
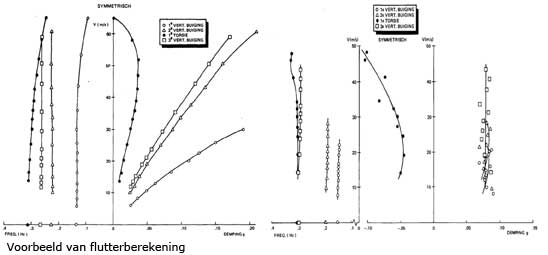
Een voorbeeld van een flutterberekening wordt getoond in onderstaande figuren. In het linker deel van de grafieken zijn de eigenfrequenties uitgezet tegen de windsnel-heid. In het rechter deel is de demping van het brugdek uitgezet als functie van de windsnelheid. Hieruit blijkt, theoretisch gezien, dat flutter optreedt boven 60 m/s (links) in de laagste torsietrillingsvorm; de demping is nu nihil (flutter onset). Maar met gemeten luchtkrachten (rechts) laat de eerste torsietrillingsvorm een negatieve demping zien, al bij regelmatig voorkomende windsnelheden. De vormgeving van dit brugdek, met name de beide kokerprofielen, veroorzaakt kennelijk bij lage windsnelheden al een aërodynamische instabiliteit. Geadviseerd werd dan ook de geometrie aan te passen en een vervolgonderzoek uit te voeren. Dit heeft echter nooit plaatsgevonden door het destijds genomen besluit, een tunnel te realiseren.
b) Pyloon
Een ander aspect van het onderzoek betrof de pyloon van de brug. Alhoewel van beton wordt in de literatuur vermeld dat dit soort constructies, ondanks een aanzienlijke constructiedemping bij relatief lage en daardoor vaak voorkomende windsnelheden in trilling kunnen geraken. Aangezien de pylonen voorafgaande aan de bouw van de overspanning een zekere tijd vrij zouden zijn opgesteld, leek het gezien de eerder berekende lage eigen frequenties niet uitgesloten dat trillingen zich voor zouden kunnen doen door wervel-excitatie (flutter wordt voor dit soort constructies uitgesloten geacht).

Om deze reden is een windtunnelonderzoek uitgevoerd aan een elastisch geschaald model (1: 60) van staal, waarbij (geringe) responsies bij een aantal windrichtingen werden vastgesteld. Met de gemeten luchtkracht coëfficiënten is via een berekeningsprocedure het res-ponsiegedrag van de betonnen pyloon op ware grootte voorspeld.

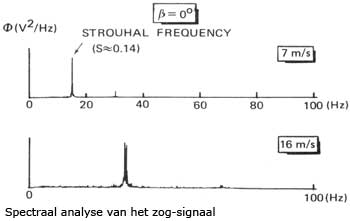
Onderdeel van het onderzoek was verder het aantonen van wervels in het zog van de pyloon. Dit is gebeurd door middel van snelheidsmetingen. Van de meetsignalen is een vermogensspectrum bepaald. Een duidelijke wervel vertoont zich als een piek in het frequentiespectrum. De frequentie van de wervel neemt lineair toe met de windsnelheid waaruit het getal van Strouhal kon worden bepaald (S = 0.14) en daarmee dus ook de windsnelheid die voor wervel-excitatie kon zorgen bij de pyloon op ware grootte.
Met behulp van rook zijn de wervels zichtbaar gemaakt, waarbij gebleken is dat alleen een duidelijke wervel achter de stroomopwaartse kolom ontstaat. Er is geen sprake van een wervelstraat achter de pyloon zelf, wat voor de responsie van een dergelijke constructie gunstig genoemd kan worden. De pyloon, als bouwfase van de Westerschelde hangbrug, heeft dan ook voldaan aan de verwachtingen.

Ten slotte

Dit artikel is tot stand gekomen op verzoek van Ir. C.Q. Klap, destijds werkzaam bij Rijkswaterstaat Directie Bruggen. Ir. Klap heeft de diverse windtunnelonderzoekingen bij het NLR aangestuurd en met interesse gevolgd. De medewerkers van de toenmalige afdeling Aëro-Elasticiteit (thans van de afdeling Aerodynamic Engineering en Trillingsonderzoek) van het NLR denken met plezier terug aan deze, ook voor hen, leerzame en interessante periode.
Literatuur
[1] Simiu, E and Scanlan, R.H.: “Wind effects on Structures”: An Introduction to Wind Engineering, A Wiley-Intersience Publication, 1978.
[2] Persoon, A.J., Siebert, C.M.: “The aerodynamic stability of the proposed Western-Scheldt suspen-sion bridge; International Conference on Flow Induced Vibrations in Fluid Engineering Reading University, England, September 1982.
Voor meer informatie: www.nlr.nl

Download hier het artikel in pdf-formaat