Bruggenstichting

A,. Romeijn

Inleiding

De boogbrug, sinds lange tijd bekend om zijn efficiënte en esthetisch fraaie constructievorm, wordt frequent in Nederland toegepast en is bij overspanningen groter dan ca. 50 m uit kostenoverweging en esthetica vrijwel enkel in staal uitgevoerd. Enkele recente toepassingen (vanaf 1997) zijn de brug over het Amsterdam Rijnkanaal, de Dintelhavenspoorbrug, de Ennaeus Heermabrug en de Demkabrug.

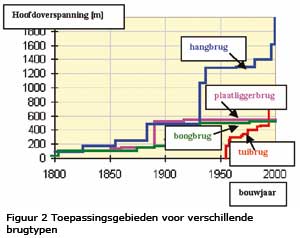De trend is, dat de rijvloer steeds meer in staalbeton wordt uitgevoerd i.p.v. enkel staal. Daarnaast wordt steeds meer ontwerpervaring verkregen met verschillende soorten beton, zoals B105 en RPC200 (vezelversterkt vloeibeton). Mogelijkerwijs zijn t.z.t. hiermee betonnen boogbruggen te construeren met een t.o.v. staaltoepassing concurrerend fraaie vormgeving. Het toepas-singsgebied van de boogbrug ligt qua overspanning tussen de ca. 50 en 500 m, waarbij als vuistregel geldt tot ca. 500 m voor verkeersbruggen en 250 m voor spoorbruggen. Bij toename van de overspanning zal de stijfheidseis van een plaat-, vakwerk- of kokerliggerbrug een steeds groter beslag leggen op het ontwerp van de brug. Dit vormt dan ook de reden voor toepassing van verstijvingen door bogen, tuien of draagkabels. Het resultaat, een boog-, tui- of hangbrug wordt daarom veelal toegepast bij grote overspan-ningen. In figuur 2 zijn voor verschillende brugtypen de toepassingsgebieden weergegeven.

HOOFDDRAAGSYSTEMEN

In essentie zijn, qua belastingafdracht, drie typen hoofddraagconstructies te onderscheiden:
• de zuivere boogbrug
• de boogbrug met trekband
• de verstijfde staafboogbrug
Naast dit onderscheid spelen verschil-lende aspecten een rol bij het bepalen van de uiteindelijke vorm van de brug. Hierbij kan gedacht worden aan:
• type belasting; wegverkeer, spoor-verkeer
• keuze van de hanger; I-profiel, kabel, koker
• hangerconfiguratie; verticaal, diagonaal, netwerk
• boogconfiguratie; enkele boog, meerder bogen, hellend boogvlak, bovenverband, eindportaal (zie fig .3)
• keuze van de rijvloer; open rijvloer, doorgaand ballastbed, orthotroop (staal), monolithisch (beton)
• architectonische eisen

Zuivere boogbrug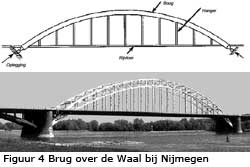

De rijvloer is relatief slap en wordt overwegend op buiging belast. De boog daarentegen is overheersend in de belastingafdracht en wordt hoofdzakelijk belast op een positief buigend moment en een drukkracht. Verder kenmerkt de brug zich door een directe afgifte van de spatkracht aan de fundering. De hanger draagt in feite alleen de belasting van de velden grenzend aan de han-ger. Hangerkrachten kunnen dan ook onderling sterk verschillen. Horizontale verplaat-singen, die de oplegpunten van de boog als gevolg van eigenge-wicht en mobiele belasting willen ondergaan, worden verhinderd door de ondersteuningsconstructie (landhoofden). De hierdoor ontstane spatkrachten veroorzaken overigens een reductie van het buigend moment in de boog. Door de verhinderde horizontale verplaatsing van de oplegpunten zal ten gevolge van een temperatuurverandering de boog zich in verticale richting moeten verplaatsen. Door deze verplaatsing ontstaat weer een extra buigend moment in de boog. De zuivere boogbrug wordt in Nederland niet zoveel toegepast omdat de bodemgesteldheid ongeschikt is voor het opnemen van horizontale belasting. Een voorbeeld van een zuivere boogbrug is de brug over de Waal bij Nijmegen.

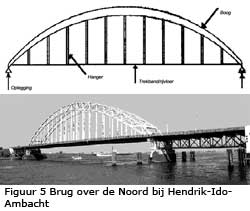Boogbrug met trekband

De boogbrug met trekband vertoont grote gelijkenis met de zuivere boogbrug. Kenmerkend verschil tussen beide hoofddraagsystemen is dat bij een boogbrug met trekband de spatkracht door een trekband opgenomen wordt in plaats van door een ondersteuningsconstructie. Deze trekband valt in veel gevallen samen met de rijvloer. Bij een dergelijke brug is één van de opleggingen vrij verschuifbaar zodat vervormingen (bijv. t.g.v. gelijkmatige temperatuurverandering) in horizontale richting ‘vrij’ kunnen optreden.
Als gevolg van de trekkracht in de trekband ondergaat de trekband een lengteverandering en veroorzaakt dus ook een verplaatsing van de roloplegging. Hierdoor ontstaat extra buiging in de boog, met als gevolg dat de spatkracht iets lager is dan bij de zuivere boogbrug. Het resulterende positieve buigende moment in de boog wordt hierdoor iets hoger. Voorbeelden zijn de brug over de Noord bij Hendrik-Ido-Ambacht en de spoorbrug bij Culemborg. De verkeersboogbruggen uitgevoerd in Nederland zijn veelal van het type boogbrug met trekband.

Verstijfde staafboogbrug

Bij een verstijfde staafboogbrug is de verstijvingsligger overheersend en wordt de ligger versterkt door een boog. Door de relatief grote stijfheid van de ligger wordt deze bij belasting niet alleen op trek, maar ook op buiging belast. De boog zorgt voor een extra versterking en wordt voornamelijk op druk belast en zal daarom slank uitgevoerd kunnen worden. Spatkrachten worden evenals bij de boogbrug via een trekband (de verstijvingsligger) kortgesloten. De hangerkracht wordt vrijwel volledig bepaald door de boogkracht, met als gevolg dat alle hangerkrachten even groot zijn. Voorbeelden zijn de brug over het Amsterdam-Rijnkanaal bij Weesp en de brug bij Schalkwijk. De verstijfde staafboogbrug wordt vaak bij spoorbruggen toegepast. In Nederland zijn slechts twee van de twintig spoorboogbruggen niet van dit type, namelijk de brug over de Rijn bij Oosterbeek en de brug over de Lek bij Culemborg.

Hangerconfiguratie

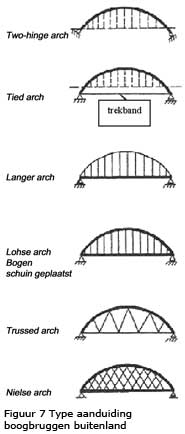
De (boogbrug) benamingen zoals in het buitenland vaak gebruikt, zijn in figuur 7 gegeven. Niet hierin getekend is het type Nielsen-Lohse. Het gaat hierbij om een com-binatie van een hangernetwerk (Nielse) met schuin-staande bogen (Lohse). Een voorbeeld hiervan is gegeven in figuur 8. Het betreft de verkeersbrug gebouwd in 1992 over het Hamadera kanaal in Osaka, Japan. De brug heeft een overspanning van 254 m en is voorzien van hangernetwerk omdat daarmee een aanzienlijke stijvere brug wordt verkregen en een sterke afname van de momenten.
De hangers hebben een veelzijdige functie. Ten eerste wordt gezorgd voor afdracht van het eigen gewicht en mobiele belasting van rijvloer naar boog en ten tweede hebben de hangers een stabiliserende werking op de boog. Voorwaarde hierbij is wel dat zowel de rijvloer als de hanger op trek is belast. Uit figuur 7 blijkt dat verschillende hangerconfiguraties bestaan. Het is in Nederland gebruikelijk om verticale hangers toe te passen. Omdat deze onder alle belastingcondities op trek belast zijn, worden daarvoor bij verkeersbruggen vaak kabels toegepast (bijv. de verkeersbrug over de Merwede bij Gorinchem). Hangers kunnen echter ook uitgevoerd worden als kokervormige of I-vormige doorsnede. Daar-naast zien we steeds vaker in Nederland dat de hangers schuin (schorend) zijn geplaatst. Dit is onder meer gebeurd bij de eerste en de tweede Van Brienenoordbrug.
De gangbare aansluitdetails hanger – rijvloer/boog ver-eisen een zekere mate van voldoende trek in de han-gers. Dit vormt vaak de reden van benodigd hoog eigen gewicht van de rijvloer.

CONSTRUCTIEF GEDRAG

Invloed hangerconfiguratie op ontwerp

De hangerconfiguratie heeft grote invloed op het ontwerp van de brug. Zo is uitgaande van het referentie-ontwerp van de Demkaspoorbrug II een vergelijkend onderzoek uitgevoerd met twee verschillende varianten in hangerconcept; verticaal en schorend.
De brug bestaat uit een stalen boog waaraan middels tuien een betonnen rijvloerconstructie is opgehangen. De boog bestaat uit gelaste stalen kokerprofielen en een doorsnede vorm zoals getekend in figuur 10. De tuien zijn opgebouwd uit 211 parallel lopende draden met een minimale breekkracht van 12690 kN.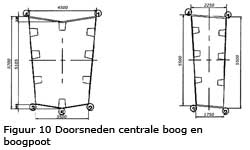
De spatkracht uit de boog wordt opgenomen door de trekband die bestaat uit dertien horizontaal geplaatste kabels gelegen onder de betonnen rijvloer.
Vijf ontwerpen met diagonaal geplaatste hangers en vijf ontwerpen met verticaal geplaatste hangers, zoals aangegeven in figuur 11 zijn met gebruikmaking van de Eurocodes doorgerekend. Hierbij is de h.o.h. afstand van de hangers gevarieerd. Tevens zijn de doorsnede-grootheden (EI, EA) van de hangers, rijvloer en boog gevarieerd. M.b.t. het ontwerp is specifiek gekeken naar de vervorming, benodigd eigengewicht rijvloer, aandeel mobiele belasting in hangerkracht, krachten in de hangers, rijvloer en boog en de invloed van de buigstijfheid boog en rijvloer.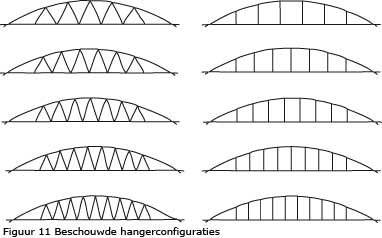

Vervorming

In figuur 12 is de verhouding tussen de totale lengte van de brug en de doorbuiging van de gehele brug uitgezet tegen de h.o.h. hangerafstand. De maximale door-buiging treedt op bij halve volbelasting van de brug, op ca. een kwart van de overspanning.

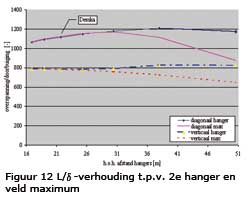Conclusies:

• Toepassing van diagonaal hangers geeft een aanzienlijk geringere doorbuiging.
• De hoek die de diagonaal hangers met de boog en de rijvloer heeft bij 5 velden de gunstigste invloed op de stijfheid. M.a.w. variatie van de h.o.h. afstand is een zinvolle exercitie.
• De invloed van de h.o.h. afstand van verticaal geplaatste hangers op de doorbuiging is gering. De stijfheid wordt bepaald door de stijfheden van de boog en de rijvloer.
• Het is zinvol dat een hanger-rijvloer aansluiting zich bevindt op een kwart van de overspanning.

Benodigd eigengewicht rijvloer

Voor ontwerp van de Demkaspoorbrug schrijft het programma van eisen voor dat de trekkracht in de tuien onder alle omstandigheden minimaal 100 kN dient te zijn. Het betreft een enigszins merkwaardige eis die vaak aan het ontwerp van hangers bij een boogbrug wordt meegegeven. Om dit te realiseren zal een bepaalde hoeveelheid massa in de rijvloer aanwezig moeten zijn, die ervoor zorgt dat de spanning in de hangers positief blijft. Verschillende argumenten kunnen een rol spelen bij een minimum waarde aan trekkracht in de hanger. Bijv. de hanger mag niet in schadelijke trilling komen (eigen frequentie is afhankelijk van de trekkracht), de hanger fungeert als knikverkorter van de bovenrand (wanneer de trekkracht nul wordt, dan fungeert de hanger niet langer als ondersteuning van de boog) en het aansluitdetail hanger – rijvloer vraagt om een permanente trekkracht.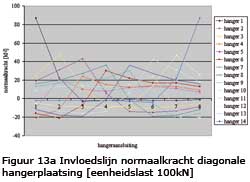

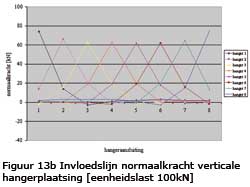
Voor beoordeling of een hanger permanent op trek is belast is het nodig de normaalkracht-invloedslijn op te stellen. In figuur 13 zijn deze invloedslijnen gegeven (hangernummering van links naar rechts) uitgaande van 7 velden.
Wanneer de invloedslijn onder de nul lijn ligt dan betekent dit dat verkeersbelasting de betreffende hanger ontlast c.q. op druk belast i.p.v. op trek. In figuur 14 is het benodigde eigengewicht voor de rijvloer weerge-geven waarbij een zekere mate van trek in de hangers aanwezig blijft.

Te concluderen is:
• Bij diagonale plaatsing van de hangers veel gewicht nodig is in de rijvloer.
• De kans dat bij verticale hangers “druk” optreedt is minimaal.
• Het toepassingsgebied voor diagonale hangers is, gezien het steile verloop van de lijn, nauw begrensd.
• De h.o.h. afstand van de hangers heeft, bij een diagonale plaatsing van de hangers, een niet te verwaarlozen invloed op het benodigde eigengewicht van de rijvloer.
• Wanneer tenminste 100 kN trek in de diagonaal han-gers aanwezig moet zijn, is voor de rijvloer van de Demkabrug een eigengewicht van minimaal 26300 kg/m nodig. De grootte van de mobiele belasting bedraagt ongeveer 180 kN/m. De verhouding eigengewicht/mobiele belasting bedraagt dan ca. 1,5:1, hetgeen hoog is.
• Bij verticale hangers bedraagt deze verhouding ca. 1,1:1.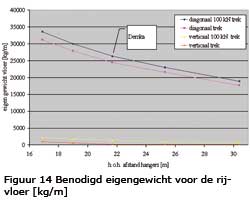

Aandeel mobiele belasting in hangerkracht

Voor het bepalen van de benodigde kabeldoorsnede moet aan een scala van factoren worden gedacht. Bijv. gewenst minimum spanningsniveau dat garant staat voor een ondergrens van fictieve elasticiteitsmodulus (formule van Ernst), aërodynamisch gedrag (met name de eigenfrequentie), vermoeiingssterkte (de spanningsrimpel) en treksterkte.
Door de karakteristieke vermoeiingsbelasting(en) op de brug te plaatsen zijn de krachtsintervallen in de hangers te berekenen. Uitgaande van statische waarden en ei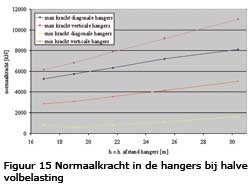gengewicht conform referentieontwerp is in figuur 15 voor halve volbelasting (maatgevend voor zowel diagonaal als verticale hangers) de maximale en minimale normaalkracht in de hangers weergegeven.
Te concluderen is:
• Diagonale plaatsing van de hangers leidt tot een groter aandeel mobiele belasting in de hangers.
• De spreiding in hangerkrachten bij diagonale plaatsing is veel groter dan bij verticale plaatsing. Dit heeft negatieve gevolgen voor de vermoeiingsanalyse.
• Uit sterkteoverweging wordt de grootte van de hangerdoorsnede bij verticale plaatsing bepaald door de maximale kracht in de hanger. Bij diagonale plaatsing echter is de kans groot dat de hangerdoorsnede wordt bepaald door de toegestane spanningsrimpel.

Krachten in de hangers, rijvloer en boog

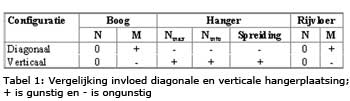
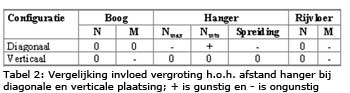
De resultaten voor de normaalkracht (N) en het moment (M) in resp. de boog, hanger en rijvloer voor de twee alternatieven van hangerconfiguratie met variatie in h.o.h. afstand van de hangers zijn samengevat in de tabellen 1 en 2.
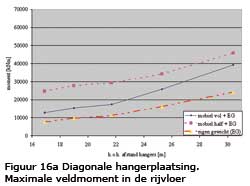
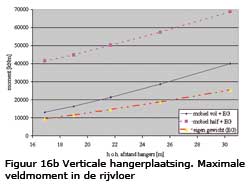
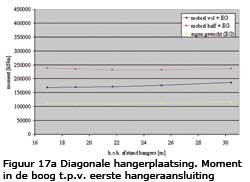
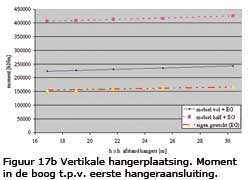
Meer gedetailleerd zijn resultaten voor het moment in de rijvloer gegeven in figuur 16 en voor het moment in de boog in figuur 17.
Uit figuur 16 en 17 blijkt dat de situatie waarbij de brug voor de helft wordt belast door mobiele belasting maatgevend is bij het ontwerp van de rijvloer en de boog . Dit geldt in het bijzonder bij toepassing van verticale hangers.

Invloed buigstijfheid boog en rijvloer

Voor de twee hangerconfiguraties is voor een aantal varianten in buigstijfheid de vervorming en krachten in de hangers, rijvloer en boog onderzocht. Op het traagheidsmoment (I-waarde) van de boog en de rijvloer na zijn alle doorsnedegrootheden constant gehouden. Voor de belastingcombinatie is gerekend met halve volbelasting.
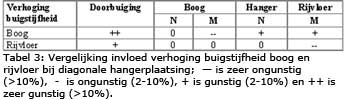
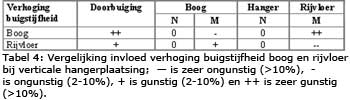
De resultaten voor de vervorming en de krachten in de boog, hanger en rijvloer voor de twee alternatieven van hangerconfiguratie staan samengevat in de tabellen 3 en 4.
Uit de tabellen 3 en 4 blijkt dat met name bij een tekort aan stijfheid van de constructie, vergroting van de buigstijfheid van de boog het meest zinvolle alternatief is.

Vervormingen

Meer gedetailleerd zijn resultaten voor de vervorming gegeven in figuur 17 en krachten in de hangers in figuur 19.
De resultaten voor de vervormingen staan afgebeeld in de figuur 18.

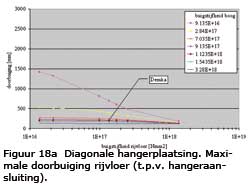
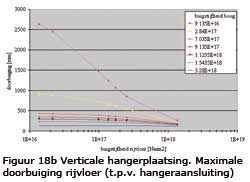
Te concluderen is:
• Bij toenemende buigstijfheid van de boog neemt de maximale doorbuiging sterk af.
• De stijfheid van de rijvloer is beperkt van invloed (met uitzondering van de varianten met een lage buigstijfheid).
• De relatieve invloed van de stijfheid van de boog is bij verticale hangerplaatsing groter dan bij diagonale hangerplaatsing.
• Om aan de eis < L/800 te voldoen is bij gelijke buigstijfheid van de rijvloer bij toepassing van verticale hangers een ca. 1.5 maal grotere buigstijfheid van de boog nodig.

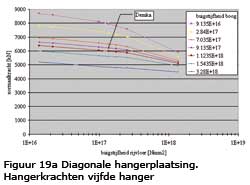
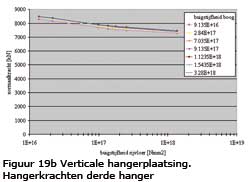
Krachten in de hangers

De maximale hangerkracht bij diagonale plaatsing treedt op in de vijfde hanger en bij verticale plaatsing in de derde hanger. De resultaten voor de hangerkrachten staan afgebeeld in de figuur 19.

Te concluderen is: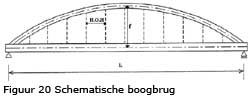
• De invloed van de buigstijfheid van de boog is bij diagonale hangerplaatsing veel groter dan bij verticale hangerplaatsing.
• Bij verticale hangerplaatsing heeft de buigstijfheid van de boog geen invloed op de buigstijfheid van de rijvloer.

Pijlhoogte f

Wanneer een boog de druklijn wil volgen, zal bij toenemende belasting van de boog de pijl van de boog ook toenemen. Bij gelijkmatig verdeelde belasting over de gehele lengte van de brug treden dan geen momenten op.
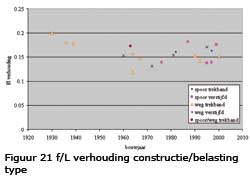
In het algemeen is de f/L verhouding voor verkeersbruggen lager dan voor spoorbruggen.
Voor de boogbuggen in Nederland is de verhouding f/L naar constructie/belasting type toegelicht in figuur 21.

Stabiliteit van de boog

Een belangrijk instabiliteitverschijnsel waarmee rekening moet worden gehouden bij het ontwerp is knik. Knik treedt op wanneer de drukkracht in de boog zo groot is dat bij een geringe zijdelingse uitbuiging de boog ‘door-knikt’ en bezwijkt. De kritische belastingswaarde voor dit knikken wordt de Eulerse knikkracht genoemd. Hierbij is het overigens belangrijk een juiste waarde voor de kniklengte te vinden. De basis formule voor de knikberekening, de Eulerse knikkracht, ziet er als volgt uit:

met: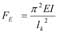
EI de buigstijfheid van de staaf in de beschouwde buigrichting
l_k de kniklengte van de staaf

Knik in het vlak, boogbrug met trekband

De kritische belastingswaarde Ncr in het vlak wordt weergegeven met de volgende formule:
met: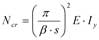
N_cr de kracht bij de opleggingen (in de boog)
s    de halve lengte van de boog
EI_y de stijfheid van de boog in het vlak
β    de kniklengte factor
De kniklengte factor voor bogen met een vol belaste
rijvloer, trekband en hangers kan bepaald worden middels figuur 22, hierin is m het aantal hangers.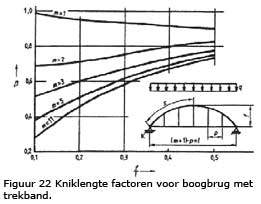
In de figuur is te zien dat bij een toenemend aantal hangers, bij gelijkblijvende f/l, de waarde van β en dus de kniklengte afneemt en zodoende de waarde van N_cr toeneemt. Een toenemend aantal hangers heeft bij een f/l van 0,1-0,2 een gunstige invloed op de kniklengte. Verder blijkt uit de lijnen dat bij toenemende f/l verhouding de waardes voor β steeds dichter bij elkaar komen te liggen. Bij grote f/l verhoudingen neemt het voordeel van meerdere hangers kennelijk af. Dit heeft te maken met de kritieke kniklengte van het eerste deel van de boog, van de geboorte tot de aansluiting met de eerste hanger.
Moet rekening gehouden worden met het uitvallen van een hanger, dan heeft dat tot consequentie dat voor de berekening van de knikfactor met de helft (of zelfs de helft min één) van het oorspronkelijke aantal hangers gerekend moet worden. Immers de hangerafstand p wordt verdubbeld zodat, bij gelijkblijvende overspanning l, de waarde (m + 1) moet halveren. Zeker bij een klein aantal hangers kan dit een behoorlijke invloed op de knikfactor hebben.

Knik uit het vlak

De kritische belastingswaarde N_cr uit het vlak voor vrijstaande bogen wordt weergegeven met de volgende formule:
met: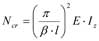
N_cr de kracht bij de opleggingen;
l     de projectie lengte van de boog;
EI_z de stijfheid van de boog loodrecht op het vlak;
β    de kniklengte factor.
Knik uit het vlak van bogen voorzien van windverband en portalen kan geverifieerd worden door een stabiliteitscontrole van de eindportalen uit te voeren.

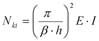
Er bestaan verschillende varianten in eindportalen. In figuur 23 is een voorbeeld gegeven van een eindportaal uitgevoerd in het vlak van de boog en een eindportaal in het vlak van de verticale hanger.
Een voorbeeld waarbij de boog vertakt en daarmee geïntegreerd tot eindportaal is gegeven in figuur 24. Het betreft het referentieontwerp van de Demkabrug.
Naast drukkrachten moet voor de bepaling van de stabiliteit ook rekening gehouden worden met momenten.
Bij knik uit het vlak bij vrijstaande bogen is de knikfactor β opgebouwd uit een tweetal factoren, β en β₂. De factor β is afhankelijk van de f/l verhouding en het traagheidsmoment (zie tabel 5).
De waarde van β₂ wordt bepaald met de formule: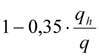
met:
q_h  is belasting overgedragen door de hangers;
q   is totale belasting.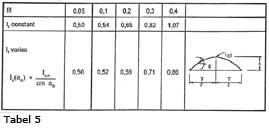
Bij toenemend belastingaandeel daalt dus de waarde van de knikfactor. De boog wordt als het ware door de hangers op zijn plaats gehouden (bij een uitwijking trek-ken de hangers de boog terug op zijn plaats).
De knikfactor β is nu te bepalen door β en β₂ met elkaar te vermenigvuldigen.

Mobiele belasting

Afhankelijk van het te ontwerpen onderdeel moet rekening worden gehouden met een viertal optredende vormen van mobiele belasting.
I: 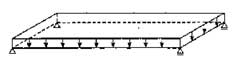 Volbelast: gelijkmatig verdeelde belasting voor beide hoofdliggers over de volledige lengte. Bijv. maatgevend voor de grootste normaalkracht in de boog
II: 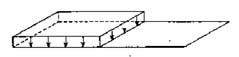 Halfbelast: gelijkmatig verdeelde belasting voor beide hoofdliggers over de halve lengte. Bijv. maatgevend voor het grootste buigend moment in de rijvloer en de grootste verticale verplaatsing van de rijvloer.
III: 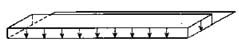 Eén spoor belast: gelijkmatig verdeelde belasting voor één hoofdligger over de volledige lengte. Bijv. maatgevend voor de grootste zijdelingse verplaatsing en buigend moment in dwarsrichting van de rijvloer.
IV: 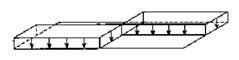 Schaakbord belast: gelijkmatig verdeelde belasting over de linkerhelft van de ene hoofdligger en de rechterhelft van de andere hoofdligger. Bijv. van belang bij ontwerp van een bovenwindverband.

Download hier het artikel in pdf-formaat